You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Universes
- Thread starterTechWench
- Start date
The DMX512 specification only allows for the control of upto 512 channels. Now with intelligent lights etc people have found now that they need more channels. To get around this problem they have made completely seperate sets of 512 channels, complete with all required protocols, which have their own plugs on the lighting console. Each group of 512 DMX channels is known as a universe and operates independently of each other. So the light controled by channel 1 on universe A is a completly different light then the lightcontrolled by channel 1 on universe b.
NB: For the specifics of the Expression III boards the information was taken from the dowloaded manual "Experssion 3 lighting control system V3.1"
On the expression III boards they don't call the seprate DMX outputs universe but ports.
To keep things simple the channel numbers run from 1 to 1536 so you don't have to remember which light is on which port. The board does it for you. By default:
Port 1 covers channels 1 - 512
Port 2 covers channels 513 - 1024
Port 3 covers channels 1025 - 1536
By going in through the "Setup Menu"l you can use the
"Output Configuration" option to change the start numbers of the ports.
For example if you had only 150 channels of convetional dimmers you may choose to have them on channel 1 through 150 on Port 1.
You may then have intelligent lighting which requires a total of less than 300 channels. To keep things simple you decide the intelligent lights can go on a separate Port (universe) so that they don't intefere with the dimmers.
You could leave the default start of Port 2 at 513 but this isn't an easy number to remember. So you might set Port 2 to start address 200 so you know any number from 200 up refers to intelligent lights. As you can define what channel each intelligent fixture starts at you might like to set them so that each individual fixture starts at a fixed multiple of channels eg say each fixture needs 16 channels you might go something like this
fixture 1 - 200
fixture 2 - 220
fixture 3 - 240 etc.
This is only a suggestion that might make easier to remember the correct channels numbers instead of having to look them up all the time.
I hope this helps answer your question.
NB: For the specifics of the Expression III boards the information was taken from the dowloaded manual "Experssion 3 lighting control system V3.1"
On the expression III boards they don't call the seprate DMX outputs universe but ports.
To keep things simple the channel numbers run from 1 to 1536 so you don't have to remember which light is on which port. The board does it for you. By default:
Port 1 covers channels 1 - 512
Port 2 covers channels 513 - 1024
Port 3 covers channels 1025 - 1536
By going in through the "Setup Menu"l you can use the
"Output Configuration" option to change the start numbers of the ports.
For example if you had only 150 channels of convetional dimmers you may choose to have them on channel 1 through 150 on Port 1.
You may then have intelligent lighting which requires a total of less than 300 channels. To keep things simple you decide the intelligent lights can go on a separate Port (universe) so that they don't intefere with the dimmers.
You could leave the default start of Port 2 at 513 but this isn't an easy number to remember. So you might set Port 2 to start address 200 so you know any number from 200 up refers to intelligent lights. As you can define what channel each intelligent fixture starts at you might like to set them so that each individual fixture starts at a fixed multiple of channels eg say each fixture needs 16 channels you might go something like this
fixture 1 - 200
fixture 2 - 220
fixture 3 - 240 etc.
This is only a suggestion that might make easier to remember the correct channels numbers instead of having to look them up all the time.
I hope this helps answer your question.
2 4 8 16 32 64 128 256 512 1024
a good sequence of numbers to know! Many many many things digital use these numbers b/c when you are working with 1s and 0s multiples of 2 work out very nicely. (you may recognize these numbers from seeing them arround your computer (RAM for instance comes in these multiples)) DMX is digital, and hey, go figure 512 channels works out nicely!
a good sequence of numbers to know! Many many many things digital use these numbers b/c when you are working with 1s and 0s multiples of 2 work out very nicely. (you may recognize these numbers from seeing them arround your computer (RAM for instance comes in these multiples)) DMX is digital, and hey, go figure 512 channels works out nicely!
so avkid said that 512 channels = 1 universe
so if i program something at say...652 that would automatically be in the second universe.. .right?
so basically, i would daisy chain my movers together and then run them into the 2nd port in the board and then start them at 512.
correct??
thanks for all of the help guys!
and Peter, how would i utilize those numbers?
are you just saying that those are good to program with/ start the lights out on those?
im confused. :?
so if i program something at say...652 that would automatically be in the second universe.. .right?
so basically, i would daisy chain my movers together and then run them into the 2nd port in the board and then start them at 512.
correct??
thanks for all of the help guys!
and Peter, how would i utilize those numbers?
are you just saying that those are good to program with/ start the lights out on those?
im confused. :?
TechWench you have got the idea. Except you would start at 513 as 512 is the last address in a DMX universe in your case this would still be on Port 1 not Port 2.
There is one thing to watch, for your example of something at channel 652. If this is the start address of a moving light the expression board can find it all right but when you set the address on the moving light itself it has to be in the range of 1 - 512 . For the board Channels 513 - 1024 subtracting 512 will give you the address you have to set on the moving light. In the example you gave of board channel of 652, if this is the start address of the light then 652 - 512 = 140. You set the address as 140 on the moving light and make sure it is on the daisy chain from Port 2.
If you use a board channel greater then 1024 you subtract 1024 from the board number instead of 512 and this will again give you the address to put on the moving light., this time on port 3.
On the fixture patch menu it actualy shows the start channel , port number/ channel number in this case the channel number is the address to set on the fixture. For your example we would see 652 2/140.
The last method might be easier but at least you know how to calculate the right addresses for fixtures on multiple universes.
I believe Peter is refering to the fact that a lot of moving lights use
dip switches that have only two positions, on or off, to set the address so they use binary to represent the decimal address.
If you go to this page it has a DMX calculator that lets you enter a decimal and shows it as a binary number and how to set it on a dip switch.
http://business.virgin.net/tom.baldwin/dmx_calculator2.html
There is one thing to watch, for your example of something at channel 652. If this is the start address of a moving light the expression board can find it all right but when you set the address on the moving light itself it has to be in the range of 1 - 512 . For the board Channels 513 - 1024 subtracting 512 will give you the address you have to set on the moving light. In the example you gave of board channel of 652, if this is the start address of the light then 652 - 512 = 140. You set the address as 140 on the moving light and make sure it is on the daisy chain from Port 2.
If you use a board channel greater then 1024 you subtract 1024 from the board number instead of 512 and this will again give you the address to put on the moving light., this time on port 3.
On the fixture patch menu it actualy shows the start channel , port number/ channel number in this case the channel number is the address to set on the fixture. For your example we would see 652 2/140.
The last method might be easier but at least you know how to calculate the right addresses for fixtures on multiple universes.
I believe Peter is refering to the fact that a lot of moving lights use
dip switches that have only two positions, on or off, to set the address so they use binary to represent the decimal address.
If you go to this page it has a DMX calculator that lets you enter a decimal and shows it as a binary number and how to set it on a dip switch.
http://business.virgin.net/tom.baldwin/dmx_calculator2.html
Binary!?
ok, ya that is VERY helpful.
ok another quick question then.
If i had say... 150 conventional dimmers, i would put those on port 1.
and then if i had 4 moving lights, would it be smart to split them up and put 2 on port 2 and the other 2 on port 3?
just to spread things out?
i feel like there would be less of a chance for errors or breakdowns...maybe im wrong though.
speaking of binary code (blech)
could you explain that to me?
ive had a few encounters with it.
but everytime i had to address it i handed it off to the TD. 8)
he explained it to me, but there was so much other stuff going on that it just slipped away from me.
i know you have to add up all of the numbers....or something like that?
ya, im lost!
oy!
You guys are great!
thanks for all of the help!
ok, ya that is VERY helpful.
ok another quick question then.
If i had say... 150 conventional dimmers, i would put those on port 1.
and then if i had 4 moving lights, would it be smart to split them up and put 2 on port 2 and the other 2 on port 3?
just to spread things out?
i feel like there would be less of a chance for errors or breakdowns...maybe im wrong though.
speaking of binary code (blech)
could you explain that to me?
ive had a few encounters with it.
but everytime i had to address it i handed it off to the TD. 8)
he explained it to me, but there was so much other stuff going on that it just slipped away from me.
i know you have to add up all of the numbers....or something like that?
ya, im lost!
oy!
You guys are great!
thanks for all of the help!
soundman1024
Active Member
You aren't understanding binary code, or base 2? I'll try to explain it starting from the beginning which you most likely know. Every number can be expressed in base 2. That means every number can be expressed as a 1 or 0. I think the easiest way to do it is to pick a number like 387. If you needed to put 387 into base 2 I would start out by writing out the powers of 2. In this case you need one greater than 387. Eventually this will be mental or memorized if you do it alot..but start out by stating the powers of 2.
1,2,4,8,16,32,64,128,256,512
You can stop at 512 because 1) that is the end of a universe and 2) that is greater than 387. Now go through those numbers and find the biggest you can that isn't more than 387. That would be 256. Since you have one 256 that can be added to get to 387 the switch for 256 is now a 1 instead of a 0
1__2__4___8 __16__32__64_128_256_512
0__0__0___0___0___0___0___0___1___0
Now subtract the 256 from 387. 387-256=131. Now you have to find 131 and you have the start of your base 2 number. Then you start going down the chain, the next smallest of the powers of 2 is 128. There is a 128 in 131, so you add the 1 there and do your subtraction.
1__2__4___8 __16__32__64_128_256_512
0__0__0___0___0___0___0___1___1___0
131-128=3
Now you check for 64. No 64s go into 3, nor does 32, nor does 16, nor does 8, nor does 4. Those would all remain as a 0. A 2 will go into 3, so you do the subtraction (3-2=1). You change your number
1__2__4___8 __16__32__64_128_256_512
0__1__0___0___0___0___0___1___1___0
Now you have 1. One does go into 1 leaving you with 0 for the number you need to get to in the end.
1__2__4___8 __16__32__64_128_256_512
1__1__0___0___0___0___0___1___1___0
After that take out the spaces to get your number.. 110000011. For the DMX address 387 you would have the first, second, eithth and nineth switchs at 1 and the rest at 0. Hopefully that helps you understand base 2.
1,2,4,8,16,32,64,128,256,512
You can stop at 512 because 1) that is the end of a universe and 2) that is greater than 387. Now go through those numbers and find the biggest you can that isn't more than 387. That would be 256. Since you have one 256 that can be added to get to 387 the switch for 256 is now a 1 instead of a 0
1__2__4___8 __16__32__64_128_256_512
0__0__0___0___0___0___0___0___1___0
Now subtract the 256 from 387. 387-256=131. Now you have to find 131 and you have the start of your base 2 number. Then you start going down the chain, the next smallest of the powers of 2 is 128. There is a 128 in 131, so you add the 1 there and do your subtraction.
1__2__4___8 __16__32__64_128_256_512
0__0__0___0___0___0___0___1___1___0
131-128=3
Now you check for 64. No 64s go into 3, nor does 32, nor does 16, nor does 8, nor does 4. Those would all remain as a 0. A 2 will go into 3, so you do the subtraction (3-2=1). You change your number
1__2__4___8 __16__32__64_128_256_512
0__1__0___0___0___0___0___1___1___0
Now you have 1. One does go into 1 leaving you with 0 for the number you need to get to in the end.
1__2__4___8 __16__32__64_128_256_512
1__1__0___0___0___0___0___1___1___0
After that take out the spaces to get your number.. 110000011. For the DMX address 387 you would have the first, second, eithth and nineth switchs at 1 and the rest at 0. Hopefully that helps you understand base 2.
soundman1024
Active Member
If you play attention you can find shortcuts like every odd number has a 1. If a number is one less than one of the base 2 factors then every factor below has a 1. I think an example would help there. Take 63 as an example.
1__2__4___8 __16__32__64_128_256_512
1__1__1___1___1___1___0___0___0___0
I'm sure there are more but those 2 come to mind right now.
1__2__4___8 __16__32__64_128_256_512
1__1__1___1___1___1___0___0___0___0
I'm sure there are more but those 2 come to mind right now.
hi so im usually using a HOG 1000 and have no issues but the client has requested that the house lights be used.
The venue tells me that the DMX addresses for these lights are 1 through to 335 so i want to put the moving lights and conventionals onto universe 2.
so please tell me if im wrong here but if im using a mac 700 on universe 2 i address the mac at 1 on the fixture and it will be patched in as 513 on the HOG???
The venue tells me that the DMX addresses for these lights are 1 through to 335 so i want to put the moving lights and conventionals onto universe 2.
so please tell me if im wrong here but if im using a mac 700 on universe 2 i address the mac at 1 on the fixture and it will be patched in as 513 on the HOG???
Not quite. Almost every console today, including the nearly fifteen year-old Hog1000 running WholehogII software, uses universe/address format, rather than absolute DMX, so that one needn't add/subtract multiples of 512. Your MAC700 would be referred to as 2/1, 2/001, 2.1, or 2.001.
In the Patch window, there are two columns, the first for Universe#1 and the next for Univ#2. I believe the only time one would or could access an address >512 is when using the "TestDMX" output screen. (Or by pressing "Absolute Address" in the Patch display.
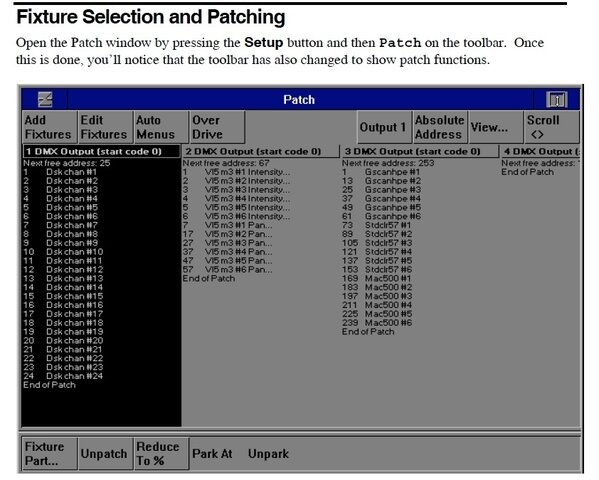
Thanks for correcting my misinformation. It has been about 8 years since I have used my board. My apologies to the OP for the error.
~Dave
~Dave
Similar threads
- Replies
- 5
- Views
- 598
- Replies
- 7
- Views
- 838
- Replies
- 21
- Views
- 1K
Automated Fixtures
Lixada mini moving head issue
- Replies
- 1
- Views
- 537
Users who are viewing this thread
Total: 1 (members: 0, guests: 1)